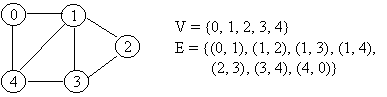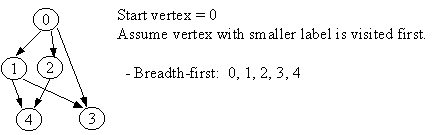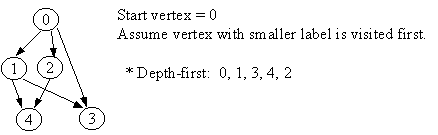Overview
- Graphs
- introduction
- graph representations
- depth- and breadth-first traversals
- Applications of depth- and breadth first search
- Dijkstra's shortest path algorithm
- Prim's minimum spanning tree algorithm
Graphs
A graph G is a pair G = (V, E) where V is a set of vertices
and E is a set of edges. Each edge e in
E is a 2-tuple of the form (v, w) where v, w in
V, and e is called an incident on v and w.
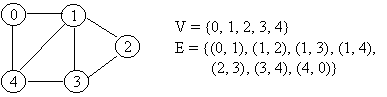
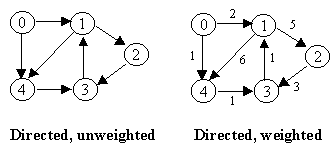
An edge may be directed or undirected.
An edge may also have a weight.
A path is a sequence of vertices
connected by edges, and represented as a sequence in 2 ways:
- (v0, e1, v1, e2,
v2,..,vn-1, en, vn)
--
alternating
vertices and edges
- (v0, v1, v2,..,vn-1,
vn) -- vertices only
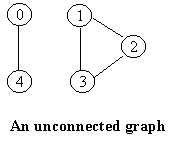
A graph is connected if, for any vertices v and w, there is
a
path
from v to w.
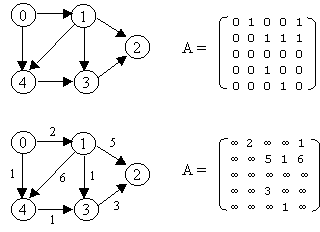
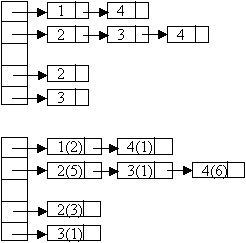
Representing Graphs
Adjacency matrix
- n by n matrix, where n is number of vertices
- A[m,n] = 1 iff (m,n) is an edge, or 0 otherwise
- For weighted graph: A[m,n] = w (weight of edge), or positive
infinity
otherwise
Adjacency list
- Adj is an array of size n, with each index i corresponding to
some
vertex i
- Each vertex i has a linked list of edges A[i]
- Edge stores destination and label
- Better when adjacency matrix is sparse
Exercise 1: Write a method
that
outputs all the edges of a graph given
using
an
- adjacency list representation
- adjacency matrix representation
Exercise 2: Write a method
that
outputs the degree of every node of a
graph
given using an
- adjacency list representation
- adjacency matrix representation
Graph Traversal
A basic functionality in any data structure is the ability to
traverse
all
the elements stored in it.
Recall that we had several traversal approaches for trees:
level
order,
pre-order, in-order, and post-order traversal.
We generalize level order traversal for trees to breadth-first traversal for
graphs.
The
only difficulty is that, in graphs we may revisit nodes because
graphs
have
cycles. To take care of this we mark nodes "unvisited" or "visited"
(once
they are visited by the traversal algorithm).
We generalize in-order traversal for trees to depth-first traversal for
graphs.
Again,
we mark nodes "unvisited" or "visited" (once they are visited by the
traversal
algorithm).
Depth-first traversal
We develop the depth-first traversal of graphs from the preorder
traversal
of trees
Here is the preorder traversal for binary trees:
public static void preorder (BTNode node)
{
System.out.println(node.element); // visit (print
the
node
data)
if (node.left != null)
preorder(node.left); // then go left
-- recursive call
if (node.right != null)
preorder(node.right); // and then go right --
recursive call
}
We generalize the preorder traversal to general trees (more than two
children
are allowed):
void preorder (TreeNode node) // pseudocode
{
print (node.element); // visit (print
the
node
data)
for every child w of node; // go to each child
preorder(w);
//
recursive call
}
How do we modify preorder so it can be used to traverse graphs?
Need to keep track of which nodes were already visited:
void DFS (GraphNode node) // pseudocode
{
print (node.element); // visit
(print
the node data)
mark node as visited;
for every unvisited neighbor w of node; // go
to
each
child
DFS(w);
// recursive call
}
}
Breadth-First Traversal
Visit nodes layer-by-layer, i.e. in the order of distance from the
start
node.
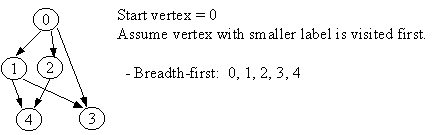
Similar to level-order traversal:
public static void levelorderIt (BTNode node)
{
Queue Q = new ArrayQueue();
Q.enqueue (node);
while (!Q.isEmpty ())
{
BTNode current = (BTNode) Q.dequeue ();
System.out.println(current.element); // visit node
if (current.right != null)
Q.enqueue (current.right); // visit right
node later
if (current.left != null)
Q.enqueue (current.left); // visit left
node next
}
}
BFS Algorithm:
Let G = (V, E) is a graph which is represented by an adjacency
matrix
Adj.
Assume that nodes in a graph record visited/unvisited
information.
procedure BREADTH-FIRST (G, s) // s is the start vertex
1. Initialize all vertices as "unvisited".
2. Let Q be a queue.
3. Enqueue s on Q.
4. While Q not empty, do
5. begin
6. n <- Dequeue Q.
7. If n is marked as "unvisited", then
8. begin
9. Mark n as "visited", and output n to the terminal.
10. For each vertex v in Adj[n], do
11. If v is marked "unvisited", then
12. enqueue v on Q.
13. end
14. end
Note that a node v may be enqueued more than once, by many of its
neighbors,
and it is dequeued as many times. Note that each instance of node v
in
Q
corresponds to a neighbor who enqueued it. Note also that when the
first
instance of node v is dequeued, node v will still be marked
unvisited.
This
instance of node v will correspond to a neighbor u of node v who, we
wil
say, discovered v. Thus, a
breadth-first
traversal implicitely constructs a breadth-first
traversal
tree consisting of all edges (u,v) such that u
discovered
v.
Depth-First Traversal
Depth-first traversal can also be implemented recursively, using a stack.
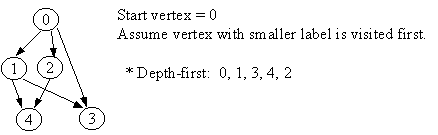
Algorithm:
Let G = (V, E) is a graph which is represented by an adjacency
matrix Adj. Assume that nodes in a graph record
visited/unvisited
information.
procedure DEPTH-FIRST (G, s) // s is the start vertex
1. Initialize all vertices as "unvisited".
2. Let S be a stack.
3. Push the start vertex on S.
4. While S not empty, do
5. begin
6. Let n <- Pop S.
7 If n is marked as "unvisited", then
8. begin
9. Mark n as "visited", and output n to the terminal.
10. For each vertex v in Adj[n], do
11. If v is marked as "unvisited", then
12. push v on S.
13. end
14. end
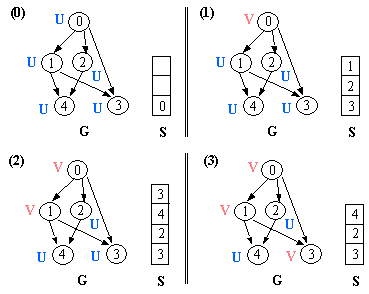
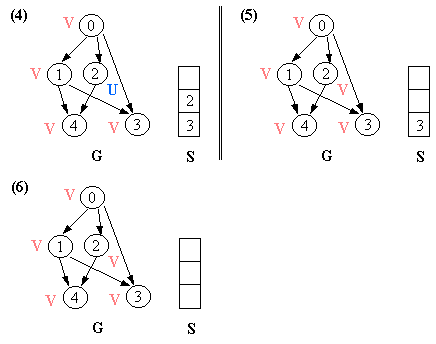
Note that a node v may be pushed more than once, by many of its
neighbors,
and it is popped as many times. Note that each instance of node v in
S
corresponds
to a neighbor who pushed it. Note also that when the first instance
of
node
v is popped, node v will still be marked unvisited. This instance of
node
v will correspond to a neighbor u of node v who, we wil say, discovered v. Thus, a
depth-first
traversal
implicitely constructs a depth-first
traversal
tree
consisting of all edges (u,v) such that u discovered v
Graph Search
Two search methods corresponding to the two traversal schemes above:
Depth-First
Search (DFS) and Breadth-First Search (BFS).
Terminate search/traversal as soon as the item is found.
A Graph ADT and its implementation
See graph
Applications of depth-first traversal
n = number of vertices
m = number of edges
Searching: find the path from a start vertex to an end vertex
- Depth-first traversal implicitely construct a DFS tree rooted
at
the
node at which the traversal started
- In order to record the edges of this tree, we define an array
of
Vertex
objects called parent
- Run depth-first traversal from the start vertex; stop the
traversal
when the end vertex is reached.
- Print the path
- Running time: O(n+m)
Example: see AbstractGraph.java in graph
Graph Connectivity: is the graph connected?
- Run depth-first traversal and mark all visited vertices as
"visited", as usual.
- Go through all the vertices and check if a vetex is is marked
"unvisited";
if so, the graph is disconnected, otherwise, the graph is
connected.
- Running time: O(n+m)
Cycle Existence: does the graph have a cycle?
- Run depth-first traversal until a back edge is found
- Running time: O(n+m)
Applications of breadth first search
Minimum spanning tree
Shortest path
- BFT can be used to compute
the lengths of the shortest paths from a given vertex to all
other
vertices. How?
- How do we compute the shortest paths themselves?
Minimum Spanning Trees (MST)
A minimum spanning tree T of an undirected graph G is a
subgraph
of G that connects all the vertices in G at the lowest
total cost.
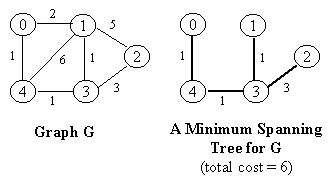
MST is used as one of the most important tools to analyze computer
networks
(e.g. cabling, network load capacity, optimal flow).
Prim's Algorithm
Just like breadth-first and depth first search, Prim's minimum
spanning
tree
algorithm will grow a tree from a given start vertex, with an edge
added
in each iteration.
The idea is to select the next edge
- which is adjacent from any vertex/node in the tree built so
far;
and
- which has the lowest weight among alternatives (i.e., all
edges
connected
from any vertex/node in the tree built so far).
Algorithm:
Let G = (V, E) which is represented by an adjacency list Adj.
Some support data structures:
- d is an array of size |V|. Each d[i]
contains
the current shortest distance from the tree to vertex i;
initially,
d[i]
= + infinity
- Q is a priority queue of UNKNOWN vertices.
- p is an array of size |V|. Each p[i] contains the
parent
of vertex i.
- s is the source vertex.
PRIM(G, s) // s is the source
vertex
1. For every v != s
initialize
d[v] and p[v] with positive
infinity and 0; initialize d[s] = 0, p[s] = 0
2. Le Q be a priority
queue
3. Q <- V // initialize Q with all vertices as UNKNOWN
4. while Q not empty do
5. begin
6. u <- ExtractMin(Q) // Q is modified
7. Mark u as
KNOWN
//
Dequeuing u is the same as marking it as KNOWN
8. for each vertex v in Adj[u] do
9. begin
10. if v is UNKNOWN and d[v] >
weight(u, v), then do
11. begin
12.
d[v]
= weight(u,
v) //
update with shorter weight
// requires a O(log n) call to
// replaceKey (see p.
342)
13.
p[v] = u // update
v's parent as u
14. end
15. end
16. end
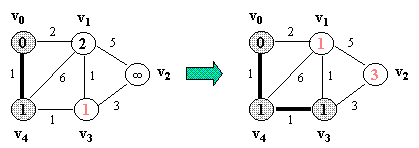
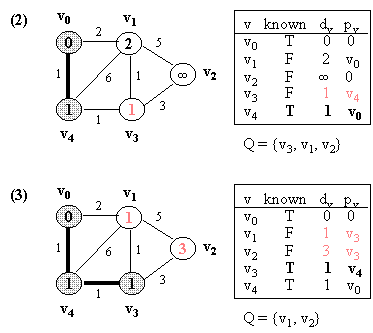
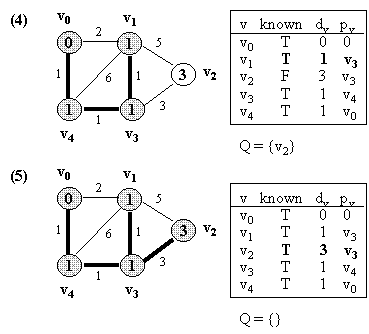
Example
(NOTE: v0 is the source vertex, and d[i] for each vertex i is also
indicated
in its circle):
Shortest Path Problem
Given a graph G = (V, E) and weights w(u,v) for every edge (u,v) in
E,
we
are interested in finding the shortest path from a given node s
(called
the
source) to a give node t.
It turns out that it is as easy to compute the shortest paths from s
to
every
node in G (because if the shortest path from s to t is s = v0, v1,
v2,
...,
vk = t, then the path v0,v1 is the shortest path from s to v1, the
path
v0,v1,v2
is the shortest path from s to v2, the path v0,v1,v2,v3 is the
shortest
path
from s to v3, etc.
We already have an algorithm to compute the shortest paths from s if
all
the edge weights are equal (say, they are all 1). Which one?
The following algorithm works as long as no edge weight is negative
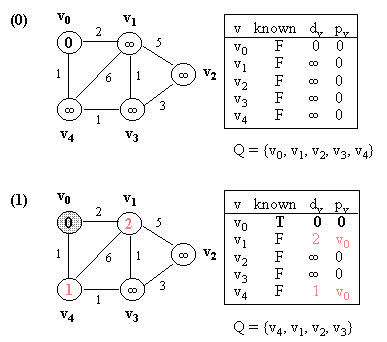
Dijkstra's Algorithm:
Let G = (V, E) which is represented by an adjacency list Adj.
Some support data structures:
- d is an array of size |V|. Each d[i]
contains
the current shortest distance from s to vertex i
- Q is a priority queue of UNKNOWN vertices.
- p is an array of size |V|. Each p[i] contains the
parent
of vertex i.
- s is the source vertex.
PRIM(G, s) // s is the source
vertex
1. For every v != s
initialize
d[v] and p[v] with positive
infinity and 0; initialize d[s] = 0, p[s] = 0
2. Le Q be a priority
queue
3. Q <- V // initialize Q with all vertices as UNKNOWN
4. while Q not empty do
5. begin
6. u <- ExtractMin(Q) // Q is modified
7. Mark u as
KNOWN
//
Dequeuing u is the same as marking it as KNOWN
8. for each vertex v in Adj[u] do
9. begin
10. if v is UNKNOWN and d[v] > d[u] +
weight(u,
v), then do
11. begin
12.
d[v]
= d[u] + weight(u, v) // update with shorter path
//
requires
a O(log n) call to
//
decreaseKey
(see p. 192)
13.
p[v]
= u // update
v's parent as u
14. end
15. end
16. end