| Contents [0/9] |
| Counting and exponentiation [1/9] |
| Counting and logarithm [2/9] |
| Fun facts [3/9] |
| Common numbers [4/9] |
| Common numbers [5/9] |
| Changing the base [6/9] |
| Approximation [7/9] |
| Order of growth [8/9] |
| Example: Computing Max [9/9] |
(Click here for one slide per page)
| Counting and exponentiation [1/9] |
We are all used to counting by adding one (arithmetic series):
0 1 2 3 4 5 6 7 ... N
You can also count by multiplying by two (geometric series):
1 2 4 8 16 32 64 128 ... N
There is correspondence between these two forms of counting, called exponentiation.
2^0 = 1 2^10 = 1024 ~ thousand (kilo/kibi)
2^1 = 2 2^20 = 1024^2 ~ million (mega/mebi)
2^2 = 4 2^30 = 1024^3 ~ billion (giga/bigi)
2^3 = 8 2^40 = 1024^4 ~ trillion (tera/tebi)
2^4 = 16 2^50 = 1024^5 ~ quadrillion (peta/pebi)
2^5 = 32 2^60 = 1024^6 ~ quintillion (exa/ exbi)
2^6 = 64
2^7 = 128
2^8 = 256
2^9 = 512
2^10 = 1024
| Counting and logarithm [2/9] |
We are all used to counting by adding one (arithmetic series):
0 1 2 3 4 5 6 7 ... N
You can also count by multiplying by two (geometric series):
1 2 4 8 16 32 64 128 ... N
There is an inverse operation, called logarithm.
People often write lg for the base 2 logarithm.
lg(1) = 0 lg(thousand) ~ 10
lg(2) = 1 lg(million) ~ 20
lg(4) = 2 lg(billion) ~ 30
lg(8) = 3 lg(trillion) ~ 40
lg(16) = 4 lg(quadrillion) ~ 50
lg(32) = 5 lg(quintillion) ~ 60
lg(64) = 6
lg(128) = 7
lg(256) = 8
lg(512) = 9
lg(1024) = 10
| Fun facts [3/9] |
These are equivalent:
N = 2^k lg(N) = k
Log and exponentiation are inverses:
lg(2^k) = k 2^lg(N) = N
Breaking up exponents and logs:
2^(k+j) = 2^k * 2^j lg(N*M) = lg(N) + lg(M)
| Common numbers [4/9] |
Since
2^(k+j) = 2^k * 2^j
we have:
2^32 = 2^2 * 2^30 ~ 4 billion (actually 4_294_967_296) 2^64 = 2^4 * 2^60 ~ 16 quintillion (actually 18_446_744_073_709_551_616)
| Common numbers [5/9] |
Since
lg(N*M) = lg(N) + lg(M)
we have:
lg(4 billion) ~ lg(4) + lg(billion) = 2 + 30 lg(16 quintillion) ~ lg(16) + lg(quintillion) = 4 + 60
| Changing the base [6/9] |
In general, logs can have any base. Generally, we write
log_b, where b is the base.
log_b(N) = log_a(N) / log_a(b)
For example, where lg(n) = log_2(n):
log_1024(N) = lg(N) / 10 --- since lg(1024) = 10
Another example, where log(n) = log_10(n):
log(N) ~ lg(N) / 3 --- since lg(10) = 3.32192809489
This video might be helpful to some:
Here's a relaxing intro to logarithms you might like:
| Approximation [7/9] |
Often details are not important
We write f(n) ~ g(n) if f and
g are more or less the same
We say f(n) is O(g(n)) if
f(n) ~ a * g(n), for some constant a
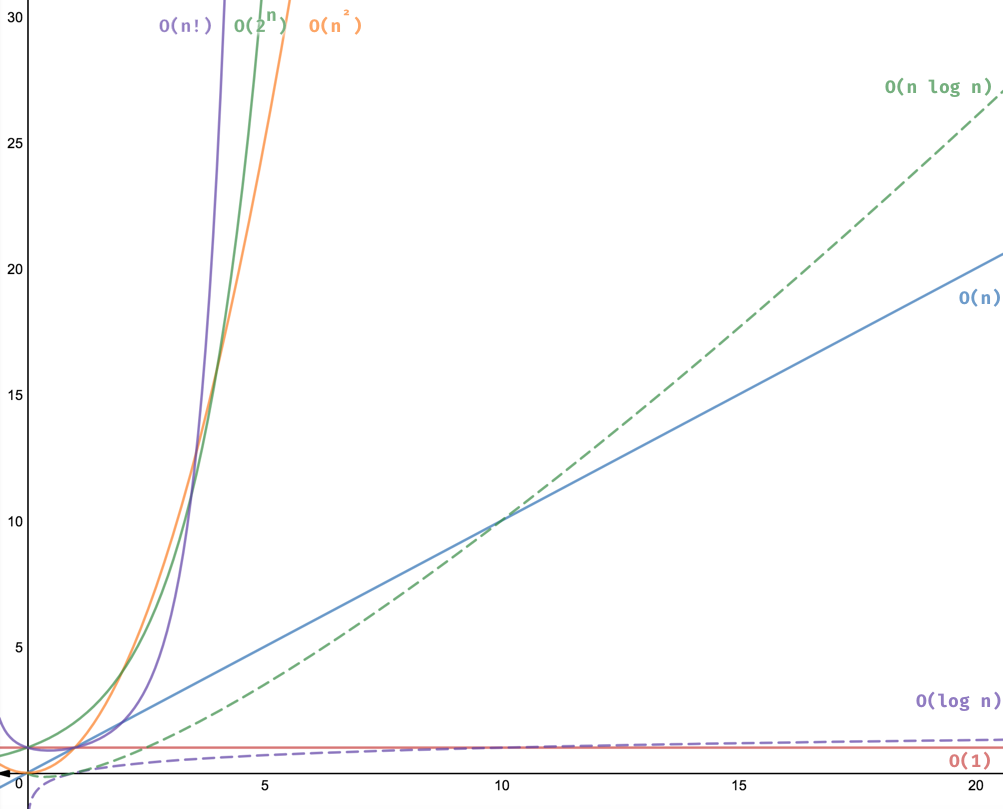
| Order of growth [8/9] |
| Name | Function | Intuition |
|---|---|---|
| Constant | O(1) | Data independent |
| Logarithmic | O(lg(n)) | Iteratively cut in half |
| Linear | O(n) | Iterate once for each item |
| Linearithmic | O(n * lg(n)) | Nested iteration: once linear, once logarithmic |
| Quadratic | O(n^2) | Nested iteration: twice linear |
| Cubic | O(n^3) | Nested iteration: three times linear |
| Exponential | O(2^n) | Combinations |
| Factorial | O(n!) | Permutations |
Image from 8 time complexities that every programmer should know by Adrian Mejia
| Example: Computing Max [9/9] |
From Week 1: Efficient way to compute max
Loop Invariant: m contains the maximum value we've seen from a[0] through a[i-1].
01 |
package algs11; import stdlib.*; public class PlaygroundMaxPerformance { public static double max (double[] a) { double m = a[0]; for (int i = 1; i < a.length; i++) { if (m < a[i]) { m = a[i]; } } return m; } } |
We say this code is efficient. Time complexity: O(n).
From Week 1: Inefficient way to compute max:
Loop Invariant (outer loop): The elements from a[0] through a[i-1] are not the max.
01 |
package algs11; import stdlib.*; public class PlaygroundMaxPerformance { public static double max (double[] a) { for (int i=0; i < a.length; i++) { boolean isMax = true; for (int j=0; j<a.length; j++) if (a[j] > a[i]) isMax = false; if (isMax) return a[i]; } throw new IllegalArgumentException(); } } |
We say this code is inefficient. Time complexity: O(n^2).