| Contents [0/29] |
(Click here for one slide per page)
| Trees: Terminology [1/29] |
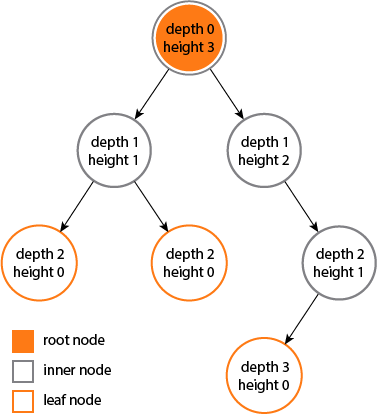
A root is a node with no ancestors.
A leaf is a node with no descendants.
Note that in a singleton tree (tree with one node), the root is also a leaf.
The size of a node is the number descendants (including itself).
A leaf node will have a size of 1.
The size of a tree is the size of its root. Empty tree has size of 0.
The height of a node is the number of edges on the longest path from the node to a leaf.
A leaf node will have a height of 0.
The height of tree is the height of its root. Empty tree has height of -1.
The depth of a node is the number of edges from the tree's root to the node.
A root node will have a depth of 0.
The depth of a tree is the same as it's height.
| Trees: Traversals [2/29] |
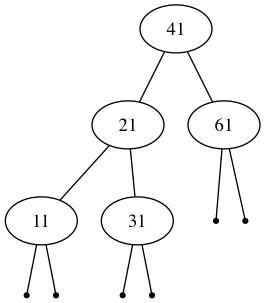
Level-order: 41 21 61 11 31
In-order: (11 21 31) 41 61
Pre-order: 41 (21 11 31) 61
Post-order: (11 31 21) 61 41
Note: Parentheses are included only for clarity.
| Tree code: While loop going left [3/29] |
public int sizeLeft () { Node x = root; int sz = 0; while (x != null) { x = x.left; sz = sz + 1; } return sz; }
While loop going left.
Here is a trace of an execution.
Back to the size problem. Here is starter code which computes the size of the leftmost branch in the tree.
| Tree code: While loop going left [4/29] |
public int sizeLeft () { Node x = root; int sz = 0; while (true) { if (x == null) break; x = x.left; sz = sz + 1; } return sz; }
A variant.
| Tree code: While loop going left [5/29] |
public int sizeLeft () { Node x = root; int sz = 0; while (true) { if (x == null) return sz; x = x.left; sz = sz + 1; } }
A variant.
| Tree code: Recursion going left [6/29] |
public int sizeLeft () { return sizeLeft (root, 0); } private static int sizeLeft (Node x, int sz) { if (x != null) { sz = sizeLeft (x.left, sz + 1); } return sz; }
Recursion going left
Here is a trace of an execution.
| Tree code: Recursion going left and right [7/29] |
public int size () { return size (root, 0); } private static int size (Node x, int sz) { if (x != null) { sz = size (x.left, sz + 1); sz = size (x.right, sz + 1); } return sz; }
Recursion going left and right. Now computing the size of the tree.
Is this correct?
Here is a trace of an execution.
| Tree code: Recursion going left and right [8/29] |
public int size () { return size (root, 0); } private static int size (Node x, int sz) { if (x != null) { sz = sz + 1; sz = size (x.left, sz); sz = size (x.right, sz); } return sz; }
Add in only once.
Here is a trace of an execution.
What is the initial value of sz at each node as we go
around the tree?
| Tree code: Recursion going left and right [9/29] |
public int size () { return size (root, 0); } private static int size (Node x, int sz) { if (x != null) { sz = sz + 1; sz = size (x.left, sz); sz = size (x.right, sz); } return sz; }
Computation of the size happens as we go forward, in a preorder traversal.
Initial value of sz at each node is the number of
nodes that precede this one in a preorder traversal.
The initial value of sz does not include the node
x.
Final value of sz is the initial value plus the size
of the tree rooted at x:
size (x, sz) returns
size (x) + sz
| Tree code: Base case first (negating the conditional) [10/29] |
public int size () { return size (root, 0); } private static int size (Node x, int sz) { if (x == null) return sz; sz = sz + 1; sz = size (x.left, sz); sz = size (x.right, sz); return sz; }
Base case first (negating the conditional)
This is more idiomatic for recursive functions.
| Tree code: Is this correct? [11/29] |
public int size () { return size (root, 0); } private static int size (Node x, int sz) { if (x == null) return sz; sz += 1; sz += size (x.left, sz); sz += size (x.right, sz); return sz; }
Is this correct?
| Tree code: Is this correct? [12/29] |
public int size () { return size (root, 0); } private static int size (Node x, int sz) { if (x == null) return sz; sz += 1; sz += size (x.left, sz); sz += size (x.right, sz); return sz; }
Is this correct?
No. size (x, sz) returns
size (x) + sz, so this is
adding it twice.
Here is a trace of an execution.
| Tree code: Is this correct? [13/29] |
public int size () { return size (root, 0); } private static int size (Node x, int sz) { if (x == null) return sz; sz = sz + 1; size (x.left, sz); size (x.right, sz); return sz; }
Is this correct?
| Tree code: Is this correct? [14/29] |
public int size () { return size (root, 0); } private static int size (Node x, int sz) { if (x == null) return sz; sz = sz + 1; size (x.left, sz); size (x.right, sz); return sz; }
Is this correct?
No. Mistake here is to think of sz as shared among
the function calls.
Here is a trace of an execution.
| Tree code: Back to sanity! [15/29] |
public int size () { return size (root, 0); } private static int size (Node x, int sz) { if (x == null) return sz; sz = size (x.left, sz); sz = size (x.right, sz); sz += 1; return sz; }
"Threaded" parameter: correct version, doing the addition postorder.
What are the initial values of sz as you go around the tree?
| Tree code: Make right call independent of the left [16/29] |
public int size () { return size (root, 0); } private static int size (Node x, int sz) { if (x == null) return sz; sz = size (x.left, 0); sz += size (x.right, 0); sz += 1; return sz; }
Make it so that the right does not know about the left!
Change so that size returns just the size of x, rather
than size of x plus sz
Intial value of sz is always 0
| Tree code: Don't need the sz parameter! [17/29] |
public int size () { return size (root); } private static int size (Node x) { if (x == null) return 0; int sz = 0; sz += 1; sz += size (x.left); sz += size (x.right); return sz; }
Don't need the sz parameter!
Node x is counted postorder, as we return.
This is true regardless of where we put sz += 1, since
the intermediate values are not passed around.
| Tree code: Local variables don't matter [18/29] |
public int size () { return size (root); } private static int size (Node x) { if (x == null) return 0; int szl = size (x.left); int szr = size (x.right); return szl + szr + 1; }
Local variables don't matter.
Here is a trace of an execution.
This is static single assignment (SSA) form: each variable is assigned on exactly one line of code.
Most compilers translate your code into SSA as part of the compilation process.
In SSA, the right-hand-side of the assignment may be restricted to be either a single function call or a single operator. In this case, the last line would be translated to:
int tmp1 = szl + szr; int tmp2 = tmp1 + 1; return tmp2;
Note: You don't need to remember SSA for exams. It's informational.
| Tree code: Local variables don't matter [19/29] |
public int size () { return size (root); } private static int size (Node x) { if (x == null) return 0; return size (x.left) + size (x.right) + 1; }
From a compiler point of view, this code is identical to the previous version, since this will be translated into SSA.
| Tree code: Nullable [20/29] |
public int size () { return size (root); } private static int size (Node x) { if (x == null) return 0; int sz = 1; sz += size (x.left); sz += size (x.right); return sz; }
Back to the version with one variable.
Note that it does not matter when we add 1 to sz,
since we don't carry the intermediate values around as parameters.
In this code, we make the call, then check for null.
The variable x is nullable (may be assigned null)
Lets call this the nullable
version.
We might also call it optimistic
, or Just do it!
| Tree code: Non-nullable [21/29] |
public int size () { if (root == null) return 0; return size (root); } private static int size (Node x) { int sz = 1; if (x.left != null) sz += size (x.left); if (x.right != null) sz += size (x.right); return sz; }
In this code, we check for null, then make the call.
The variable x is non-nullable (must not be assigned null)
Lets call this the non-nullable
version.
We might also call this cautious
, or Look before you leap!
| Tree code: The winner is... [22/29] |
public int size () { return size (root); } private int size (Node x) { if (x == null) return 0; int sz = 1; sz += size (x.left); sz += size (x.right); return sz; } |
public int size () { if (root == null) return 0; return size (root); } private int size (Node x) { int sz = 1; if (x.left != null) sz += size (x.left); if (x.right != null) sz += size (x.right); return sz; } |
What are the advantages of each approach?
In general, which should you prefer?
Nullable has one static conditional (if
statement). Non-nullable has three!
However, we have exactly the same number of dynamic
conditionals (executions of the if statement).
Nullable has about twice as many dynamic function calls! Count them!
| Tree code: The winner is... [23/29] |
public int size () { return size (root); } private int size (Node x) { if (x == null) return 0; int sz = 1; sz += size (x.left); sz += size (x.right); return sz; } |
public int size () { if (root == null) return 0; return size (root); } private int size (Node x) { int sz = 1; if (x.left != null) sz += size (x.left); if (x.right != null) sz += size (x.right); return sz; } |
nullable
version has less redundancy. Easier to maintain. Full of win.
non-nullable
version is also known as Too many base cases!
.
Only prefer performance over maintainability if you have determined that the performance is an actual problem and you have done profiling to determine the actual location of the problem.
One of the trickiest things for Java programmers is to keep track of when a variable is nullable.
Newer languages such as
swift
and
kotlin
distinguish nullable and non-nullable types. In these languages, a
variable that may be null must be given a type that ends in a
question mark. (In swift, null is written
nil, or equivalently as Optional.none.)
In these languages, we would give different types to the argument
in the helper function above. For the nullable version, x
would be given type Node? whereas for the non-nullable
version, it would be given type Node.
| Tree code: Negligent! [24/29] |
public int size () { return size (root); } private static int size (Node x) { int sz = 1; if (x.left != null) sz += size (x.left); if (x.right != null) sz += size (x.right); return sz; }
What's wrong with this code?
| Tree code: Paranoid! [25/29] |
public int size () { if (root == null) return 0; return size (root); } private static int size (Node x) { if (x == null) return 0; int sz = 1; if (x.left != null) sz += size (x.left); if (x.right != null) sz += size (x.right); return sz; }
What's wrong with this code?
| Tree code: Returns too quickly! [26/29] |
public int size () { if (root == null) return 0; return size (root); } private static int size (Node x) { if (x.left != null) return 1 + size (x.left); if (x.right != null) return 1 + size (x.right); return 1; }
What's wrong with this code?
| Tree code: "Threaded" parameter with non-nullable pointer 0 [27/29] |
public int size () { if (root == null) return 0; return size (root, 0); } private static int size (Node x, int sz) { sz = sz + 1; if (x.left != null) sz = size (x.left, sz); if (x.right != null) sz = size (x.right, sz); return sz; }
"Threaded" parameter with non-nullable pointer.
| Tree code: "Threaded" parameter with non-nullable pointer 1 [28/29] |
public int size () { if (root == null) return 0; return size (root, 1); } private static int size (Node x, int sz) { if (x.left != null) sz = size (x.left, sz + 1); if (x.right != null) sz = size (x.right, sz + 1); return sz; }
Describe the difference from the previous version.
Is it correct?
What's the invariant as we go through the tree?
| Tree code: Deriving non-nullable code from a loop [29/29] |
public int size () { if (root == null) return 0; return size (root, 1); } private static int size (Node x, int sz) { if (x.left != null) sz = size (x.left, sz + 1); if (x.right != null) sz = size (x.right, sz + 1); return sz; }
This is what you get if you start with a variant of the loop sizeLeft.
Recall the original code. Here, you count the node referenced by x.
public int sizeLeft () { Node x = root; int sz = 0; while (x != null) { x = x.left; sz = sz + 1; } return sz; }
In the following variant, we assume that x is already taken care
of, and you work on x.left instead.
public int sizeLeft () { if (root == null) return 0; Node x = root; int sz = 1; while (x.left != null) { x = x.left; sz = sz + 1; } return sz; }
Note that x is non-nullable.
It hangs back
one place.
Going recursive.
public int sizeLeft () { if (root == null) return 0; return sizeLeft (root, 1); } private static int sizeLeft (Node x, int sz) { if (x.left != null) { sz = sizeLeft (x.left, sz + 1); } return sz; }
Left and right.
public int size () { if (root == null) return 0; return size (root, 1); } private static int size (Node x, int sz) { if (x.left != null) sz = size (x.left, sz + 1); if (x.right != null) sz = size (x.right, sz + 1); return sz; }